机器学习笔记

• 通过模型和算法，训练数据（数据集），使得投喂未知数据样本（测试集）时，可以判断结果（标记label）
• 机器学习的目标是使得学到的模型能很好的适用于“新样本”,
  而不仅仅是训练集合，我们称模型适用于新样本的能力为泛化(generalization)能力
• |f(x)-y|<=e f(x)是模型结果 y是真实值 所要做的就是努力缩小两者之间的差
• 每个属性作为一个维度，想象成坐标的形式，最终的标签label，就可以指向，即视作一个向量。
• 模型假设、评价函数（损失/优化目标）和优化算法是构成模型的三个关键要素。
• 决策树
• 神经网络
• 支持向量机SVM和核方法
• 深度学习

预测内容及解决方法:

对于预测问题，可以根据预测输出的类型是连续的实数值，还是离散的标签，区分为回归任务和分类任务。

• 分类问题(classification) 二分类0/1 多分类，多是离散值但可以用联系函数连续化。常见的联系函数是
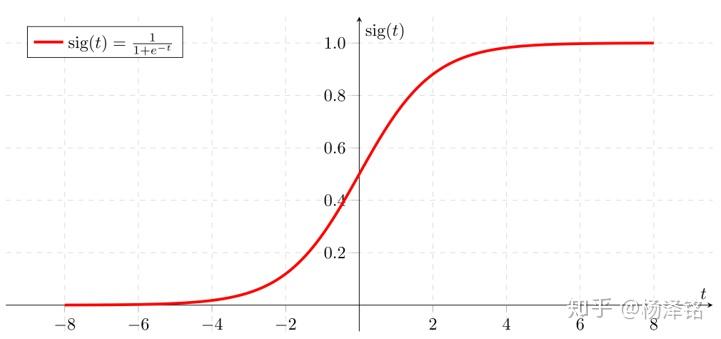
  • 决策树
  • 贝叶斯
  • 支持向量机
  • 逻辑回归
  • 集成学习
• 回归(regression)
  • 线性回归（线性的，非线性的 二次，对数ln.. ），连续值
  • 岭回归
  • Lasso回归
• 聚类问题
  • K-means
  • 高斯混合聚类
  • 密度聚类
  • 层次聚类
  • 谱聚类

基本术语

• 样本(sample)
• 属性(attribute)/特征(feature)
• 标记/标签(label)
• 真相(ground truth) 标签y的真实值
• 预测(prediction) 根据得到的模型，投入测试集预测出f(x)
• 推理(inference)
• 数据集(data set) 数据集划分为三个内容
• ①训练集(training set) 用于确定模型参数。
• ②验证集(validation set) 用于调节模型超参数（如多个网络结构、正则化权重的最优选择）
• ③测试集(test set) 将其投入到最终生成的模型中，进行测试（跑分）
• 学习器(learner) 算法程序进行特征->标签的映射
• 监督学习(supervised learning) 训练时样本给定正常答案的label，用于训练模型
• 无监督学习(unsupervised learning) 样本是没有标定label的，多用于将样本分堆
• 半监督学习
• 假设函数（Hypothesis Function）假设函数是指，用数学的方法描述自变量和因变量之间的关系，它们之间可以是一个线性函数或非线性函数。
• 损失函数（Loss Function）损失函数是指，用数学的方法衡量假设函数预测结果与真实值之间的误差。这个差距越小预测越准确，而算法的任务就是使这个差距越来越小。———-在回归问题中常用均方误差作为损失函数，而在分类问题中常用采用交叉熵（Cross-Entropy）作为损失函数
• 优化算法（Optimization Algorithm）

归纳偏好

• 没有免费的午餐 No Free Lunch
• NFL定理：一个算法a如果在某些问题上比另一个算法b好，必然存在另一些问题，b比a好
• 所以要具体问题 具体分析

模型评估方法

• k折交叉验证法
• 留出法
• 自助法

梯度下降法

• 梯度下降法 确定损失函数，随机一个起始点，使学习率慢慢变小，使得梯度一直下降，直到近似拟合，找到全局最优点
• 一.批量梯度下降
• 二.随机梯度下降SGD
  • 由于参数每次只沿着梯度反方向更新一点点，因此方向并不需要那么精确。一个合理的解决方案是每次从总的数据集中随机抽取(可以先打乱样本np.shuffle,再顺序抽取minibatch)出小部分数据来代表整体，基于这部分数据计算梯度和损失来更新参数。
  • 随机梯度下降加快了训练过程，但由于每次仅基于少量样本更新参数和计算损失ii，所以损失下降曲线会出现震荡。
• 三.小批量梯度下降

核心概念如下

• minibatch：每次迭代时抽取出来的一批数据被称为一个minibatch。
• batch size：每个minibatch所包含的样本数目称为batch size。
• Epoch：当程序迭代的时候，按minibatch逐渐抽取出样本，当把整个数据集都遍历到了的时候，则完成了一轮训练，也叫一个Epoch（轮次）。启动训练时，可以将训练的轮数num_epochs和batch_size作为参数传入。
• 也就是说 假设有400个样本，minibatch的size为40，需要遍历迭代10次才完成1轮epoch

线性模型

f(x)=w1x1+w2x2+..+wdxd+b

向量形式即f(x)=wTx+b 即模型要学习的参数是w,b

线性回归模型使用均方误差作为（Mean Squared Error，MSE）损失函数（Loss）

• 线性回归的本质就是一个采用线性激活函数的全连接层（fully-connected layer）
• 最小二乘法 多元线性回归。用到求导=0取极值的方法。但是这种方法只对线性回归这样简单的任务有效。如果模型中含有非线性变换，或者损失函数不是均方差这种简单的形式，则很难通过上式求解 就要用到普适的梯度下降法
• 对率回归 用回归的模型做二分类 可用极大似然法求解
• 线性判别分析 LDA （二分类）将二维的样例投影到一条直线上，实现降维。使同类样例的投影点尽可能接近，使异类样例的投影点尽可能远离
• 类别不平衡

决策树模型

决策树学习的关键在于如何选择最优划分属性，我们希望决策树的分支结点所包含的样本尽可能属于同一类别，即结点的“纯度”(purity)越来越高。有三种基本的划分选择

划分选择

• 一信息增益 用到信息熵的概念 对每个属性求信息增益（差值），某属性a的信息增益越大，则意味着使用属性a来进行划分所获得的“纯度提升”越大，因此用属性a来分支的优先级更大
• 二增益率 用信息增益/分支数，将两者结合，所想要的是信息增益高的同时，分支数尽量少。但并非绝对，所以使用了一个启发式：先从候选划分属性中找出信息增益高于平均水平的属性，再从中选取增益率最高的。
• 三基尼指数

剪枝

“剪枝”是决策树学习算法对付“过拟合”的主要手段。

即可通过“剪枝”来一定程度避免因决策分支过多，以致于把训练集自身的一些特点当做所有数据都具有的一般性质而导致的过拟合

• 预剪枝 生成决策树的同时剪枝
• 后剪枝 生成完整决策树后，再剪枝

需要评估剪枝前后决策树的优劣性

样本缺失值的处理

思路：样本赋权，权重划分..

神经网络

卷积神经网络

• 多用于图像识别分类领域
• 卷积核
• 卷积-（激活函数）-池化- 卷积-池化—–最后全连接神经网络

支持向量机